비계층적 군집분석(Non-hierachical Clustering)은 주어진 데이터를 k개의 군집으로 나눈다. 원하는 군집의 수 k는 사전에 지정 (알고 있다고 가정) 한다.
k-평균 군집화 알고리즘은 군집의 중심이 되는 k개의 seed(씨드) 점들을 선택하여 그 seed 점과 거리가 가까운 개체들을 그룹화하는 방법이다. 알고리즘은 다음과 같다.
- K개의 중심점을 임의로 배치한다.
- 모든 자료와 K개의 중심점과 거리를 계산하여 가장 가까운 중심점의 군집으로 할당한다.
- 군집의 중심을 구한다. (평균을 구한다.)
- 정지규칙에 이를 때까지 2~3단계를 반복한다.
- 군집의 변화가 없을때
- 중심점의 이동이 임계값 이하일 때
- 왜곡값(distortion, 각각의 클러스터의 거리제곱의 총합) 줄어들었다가 다시 늘어나는 지점
K-means 군집분석 단계는 다음과 같다.


K-means 클러스터 개수 K는 사전에 정해야 하며 결과는 K 값에 크게 영향을 받는다. 다른 K 값을 이용한 시뮬레이션을 통하여 최선의 선택을 시도해야 한다.
Elbow method는 팔꿈치처럼 가파른 경사로부터 완만하게 변하는 변곡점을 최적의 K로 제안한다.

Silhouette coefficient method는 모든 개체에 대한 Silhouttte 값을 계산, 확인하고 클러스터 별로 그 값의 분포를 검토하는 방식으로 유효성을 검토한다. Silhouette coefficient는 숫자가 큰 것을 선택한다.



Elbow Method와 Silhouette coefficient method를 비교하면 다음과 같다. Elbow method는 항상 판별이 용이한 팔꿈치가 제시되는 것은 아니다.

K-means 군집의 특징은 군집 대상에 대한 적절한 정보와 이해가 필요하고, 적정한 K 값을 지정하기 위한 다양한 시도가 요구된다. K-means clustering은 어떤 경우에 잘 작동할까?

K-means 군집분석의 특징을 정리하면 다음과 같다.
- 장점
- 대용량 데이터에 대한 탐색적 분석
- 적용이 용이하고 수행이 빠름
- 언제나 Cluster가 나누어짐 - 단점
- 최소 지역 최적화는 달성하지 못하지만 전역 최적화는 장담하지 못한다.
- 의미없는 Cluster가 형성될 수 있다.
- 결과해석이 어렵다.
- 목적에 맞는 변수를 제공해야 한다.
- 이상값에 민감하다. (평균으로 정해지므로)
< 예제 >
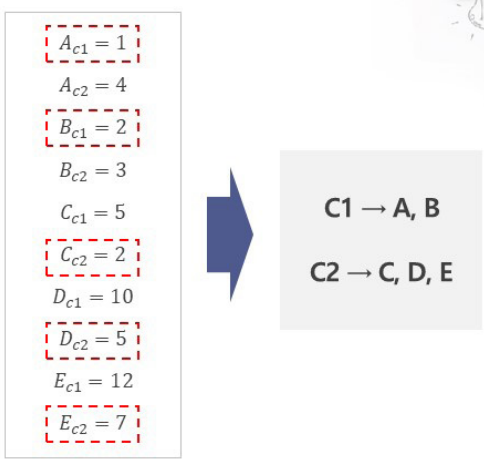
주어진 각 좌표값이 다음과 같을 때 비계층적 군집분석을 사용하여 두 개의 클러스터로 좌표를 묶으려고 한다. 클러스터의 중점이 각각 C1(1,1), C2(3,4) 일 때 C1, C2에 속하는 좌표는 무엇인가? (맨해튼 거리 사용)

비계층적 군집분석: K-means, K=2
거리는 맨하튼을 사용한다.
A와 C1, A와 C2의 맨해튼 거리를 구해서 가까운 클러스트를 선택 : C1
B와 C1, B와 C2의 맨해튼 거리를 구해서 가까운 클러스트를 선택 : C1
C와 C1, C와 C2의 맨해튼 거리를 구해서 가까운 클러스트를 선택 : C1
'데이터사이언스 > 머신러닝' 카테고리의 다른 글
| 군집 분석 (Clustering) (0) | 2023.04.23 |
|---|---|
| 의사결정나무 (Decision Tree) (2) | 2023.04.22 |
| 특성공학 (Feature Engineering) 모델평가기법 (0) | 2023.04.21 |
| 머신러닝 (Machine Learning) 개요 및 유형 (0) | 2023.04.20 |
| 특성공학 (Feature Engineering) 언더피팅 / 오버피팅 (0) | 2023.04.20 |




댓글