의사결정나무(Decision Tree)는 의사결정 규칙 (Decision Rule)을 나무구조로 도식화하여 관심대상이 되는 집단을 몇 개의 소집단으로 분류(Classification)하거나 예측(Regression)하는 계량적인 방법이다. 분류 또는 예측이 나무구조의 if ~ then 형태의 추론적으로 표현되기 때문에 다른 분석 방법에 비하여 이해와 설명이 쉽다.

의사결정나무의 구조와 용어는 다음과 같다.
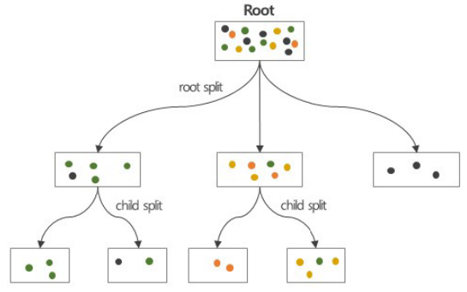
- Root node (근노드) : 모든 자료를 포함하고 있는 의사결정나무의 출발점(꼭대기)으로 자료를 몇 개의 동질적인 그룹으로 나눔
- Leaf node (잎노드) : 최종 결과를 나타내는 마디로 자료들은 더 이상 나누어지지 않음. Terminal node(단말노드)라고 함. 이 위치에 target value가 위치한다.
- Internal node : Root node와 leaf node에 위치하는 노드
- Parent/Child node : 상위 노드 / 하위 노드
- Splitting : 의사결정 노드를 주어진 기준에 따라 하위 노드로 나누는 것
- Branch/Sub Tree : 나무를 나누어 생성된 하위 나무
- Depth : root node부터 leaf node까지의 중간 마디들의 수

의사결정나무는 분류, 회귀에 모두 사용할 수 있다.
- 분류나무
. 범주형 목표변수를 기준으로 마디를 나눔
. 끝마디에 포함된 자료의 범주가 분류 결과값 (target value)이 됨 - 회귀나무
. 연속형 목표변수를 기준으로 마디를 나눔
. 끝마디에 포함된 자료의 평균값이 각 끝마디의 회귀값이 됨
의사결정나무 알고리즘은 불순도를 감소시키는 방향으로 분리 (Impurity 감소 = Purity 증가) 한다. 현재 보고 있는 데이터셋의 target value가 모두 같은 값으로 되어 있으면 decision tree 알고리즘은 stop, 만약 하나라도 섞여있으면 tree는 분기되고 데이터셋은 segmentation (단편화) 된다. 다시 각각의 데이터 셋을 보면서 target value를 보면서 반복한다.
- Step1: 모든 자료를 포함한 root node로 부터 시작한다.
- Step2: 자료 가운데 불순도를 낮추는 최적의 요인을 찾는다.
- Step3: root node를 최적 요인의 기준값을 찾아 하위그룹으로 나눈다.
- Step4: 각 하위 그룹에 대한 의사결정나무의 마디를 만든다.
- Step5: 반복적으로 새로운 child node에서 최적의 요인과 기준값을 찾고 그룹을 만든 후 하위 그룹에 대한 의사결정나무의 마디를 만든다. (Step3 ~ Step4) 이 과정을 더 이상 마디를 나눌 수 없을 때까지 혹은 정지규칙에 해당할 때까지 반복한다.
의사결정 알고리즘의 장단점을 정리하면 다음과 같다.
- 장점
- 시각화를 통한 쉬운 이해
- 자료 가공이 거의 필요없음
- 수치형 및 범부형 데이터 모두 적용 가능
- 선형성, 정규성 등의 가정이 필요 없는 비모수적 방법
- 대량 데이터 처리에도 적합 - 단점
- 휴리스틱(그럴듯한, 어림잠아)에 근거한 실용적인 알고리즘으로 전역 최적화를 얻지 못할 수 있음
- 과적합이 쉽게 발생
- 자료에 따라 불안정함 (특히 적은 자료, Class 수에 비교하여 학습 데이터가 적은 규모이면 높은 분류 에러 발생)
- Feature 간의 복잡한 관계를 처리하지 못함
- 자료가 복잡하면 실행시간이 급격히 증가
Feature select & Split 은 불순도를 최소화하는 방향으로 분류 기준(Split)을 정하고, 데이터를 나눌 때 얼마나 덜 섞이느냐를 봐야 한다.

각 변수별로 값을 바꾸어 가면서 불순도를 비교 (Brute Force Exploration)하여 불순도를 최소화하는 기준 (Feature select & value) 선택하고 반복하여 의사결정나무 구성을 구성한다.

불순도(Impurity)를 줄일 때 사용하는 척도는 다음과 같다.
- 범주형 목표변수 (Classification) : 각 범주에 속하는 빈도에 기초하여 분리한다.
- Entropy/Reduction
- Gini Reduction
- Chi-square test - 연속형 목표변수 (Regression) : 목표 변수의 평균에 기초하여 분리한다
- F-test
- Reduction of Variance

일반적으로 엔트로피(Entropy)를 많이 사용한다. 확률을 구해서 로그를 씌우고 곱하면 된다. 지니 불순도(Gini Impurity)도 확률을 쓰는데, 확률에 대해 제곱을 하여 다 더한 다음 1에서 빼주면 된다. 지니 불순도는 불순도가 작으면 작을수록 분류가 잘되어 있다고 얘기한다. 지니 값이 작으면 작을수록 좋다. 엔트로피는 최대가 1이고, 지니는 0.5이다. Variance는 분산을 이용하는 개념으로 작으면 모여있는 거고 크면 떨어져 있는 거로 보면 된다.
< 예제 > 불순도 (Impurity Measure)
지금 기침을 했을 때 감기냐? 아니냐를 분류하는 문제이다. 트리안에서 IG (Information Gain, 종합 불순도)를 구하세요.

I.G. = Gini(부모) - ( C1의 확률 * C1의 지니값 + C2의 확률 * C2의 지니값 )으로 구한다. 확률은 전체 중의 몇 개이며, YES: 86+52=138, NO: 29+33 =>62, n은 200이다.
Gini(부모) = 1 - (138/200)^2 - (62/200)^2 = 0.4278
C1의 확률 = 115/200
C1의 지니값 = 1 - (86/(86+29))^2 - (29/(86+29))^2 = 0.377
C2의 확률 = 85/200
C2의 지니값 = 1 - (52/(52+33))^2 - (33/(52+33))^2 = 0.475
C1의 확률 * C1의 지니값 + C2의 확률 * C2의 지니값 = 0.4187 정도 나온다.
Gini(부모) - 0.41865을 빼주면 종합불순도를 계산할 수 있다.
답: IG (Information Gain, 혹은 종합불순도) = 0.4278 - 0.41865 = 0.00915
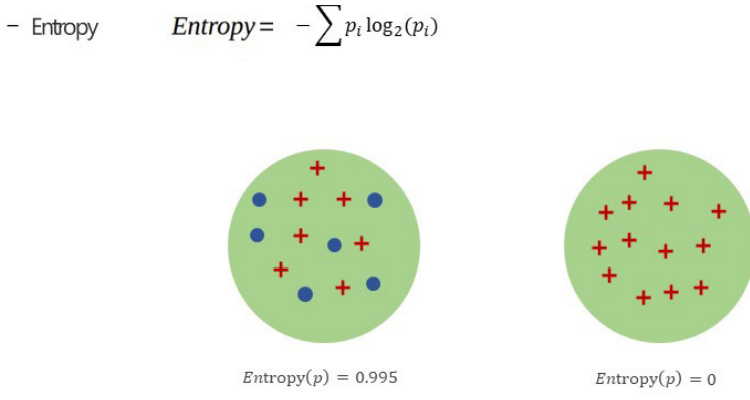
다음 그림은 엔트로피를 보여주고 있다. 엔트로피가 1에 가까울수록 거의 동수로 섞여 있게 된다. 물리학에서는 이 상태가 stable 한상태를 말한다. 플러스, 마이너가스 같은 수로 있는 상태이다. 엔트로피가 0에 가까울수록 분류가 잘되어 있다. 한쪽은 완전히 마이너스, 한쪽은 완전히 플러스만 들어가 있는 상태이다.
과적합 (Overfitting)은 지금 보고 있는 데이터에 대해서는 좋은 결과를 내나 새로운 데이터에 대해서는 정확한 예측을 못하는 것으로 다음 경우에 발생한다. 이때 해결하는 방법은 데이터를 더 넣어서 해결한다.
- 학습 데이터가 부족한 경우
- 학습 데이터에 잡음이 있는 경우
- 학습 데이터에 너무 특화되는 상황
Decision Tree 입장에서 약점은 stop 조건이 현재 보고 있는 노드의 target value가 모두 같은 경우인데 이걸 미리 멈출 방법이 없을까? 이럴 경우 모델은 좀 더 단순해진다.
Early Stopping Rule (정지규칙)은 다음과 같다.
- 모든 마디가 순수한 상태가 되면 정지
- 노드의 모든 데이터가 하나의 클래스만 남음 (순도 100% 인 경우) - 의사결정나무가 완전히 다 자라기 전에 정지하도록 하여 과적합을 방지하거나 지나치게 긴 실행 시간을 제한할 수 있음
- 트리의 깊이(depth)가 지정한 값 (Max depth)에 도달할 경우
- 노드의 크기가 지정한 값 (Max instance per node) 보다 작을 경우
- 불순도의 감소량이 지정된 값 (Min information gain) 보다 적을 경우
처음 보는 데이터의 경우 중간에 정지하도록 할 수 없다. 이럴 경우 Prunning (가지치기)을 하게 된다. Tree를 끝에서부터 가지를 치며 올라간다. 올라갈수록 모델은 단순해지며, 성능이 상대적으로 덜 떨어지는 지점까지 올라간다.
- 의사결정나무가 끝까지 자라도록 한 후 상향식으로 가지치기 실행한다. 트리의 폭이 좁아지고 깊이가 낮아진다.
- 가지치기 결과로 generalization error 가 개선되면 sub-tree를 마디로 대체
- 해당 끝마디의 클래슨느 sub-tree 클래스의 다수결로 결정
의사결정나무(decision tree)를 사용할 때 변수들이 들어오는데 어느 변수가 중요한 변수일까? 일반적으로 Tree 상단에 나오는 변수, 자주 사용되는 변수, 혼잡도 개선효과가 높은 변수이다. 그러나 상단에 나온다고 해서 반드시 중요하다는 것은 아니다. 조건부 확률처럼 전체 데이터에서는 중요하지 않았지만 데이터가 조각이 났을 경우 그 조각 안에서는 중요한 것으로 차지할 수 도 있기 때문이다.

'데이터사이언스 > 머신러닝' 카테고리의 다른 글
| 비계층적 군집분석 (Non-hierachical Clustering) (0) | 2023.04.24 |
|---|---|
| 군집 분석 (Clustering) (0) | 2023.04.23 |
| 특성공학 (Feature Engineering) 모델평가기법 (0) | 2023.04.21 |
| 머신러닝 (Machine Learning) 개요 및 유형 (0) | 2023.04.20 |
| 특성공학 (Feature Engineering) 언더피팅 / 오버피팅 (0) | 2023.04.20 |




댓글