비지도 학습 (Unsupervised Learing)은 입력 데이터에 Label 없이 데이터의 특성만으로 패턴을 찾는 학습 방법이다. 대부분은 지도학습이다. 비지도 학습을 사용하는 이유는 다음과 같다.
- 알려지지 않은 모든 종류의 패턴을 찾으려는 시도
- 범주화에 도움되는 특징과 패턴을 알아내는데 도움이 됨
- 새로운 데이터에 대한 실시간으로 처리 가능
- Label이 되지 않는 데이터가 더 확보하기 쉬움. 라벨링에 비용과 시간이 많이 든다.
비지도 학습의 종류에는 Clustering, Association Rule, Dimension Reduction 등이 있다.
Clustering (군집분석)은 계층적 군집분석과 비계층적 군집분석이 있다. Clustering은 주어진 입력값(들)을 바탕으로 유사한 값들로 데이터를 몇 개의 그룹으로 묶어주는 것이다. KNN도 거리를 기반으로 간다. 각 집단의 성격을 파악하여 데이터 전체의 구조에 대한 이해를 높이는 탐색적 분석방법이며, 비지도 학습의 하나로 분석가의 해석이 중요하다. 사전에 정의되거나 가정하는 사항 없이 데이터에 의존하는 분석 기법이며, 점포 세분화 고객관리를 위한 구분, 가맹정 세분화 등에 널리 사용된다.

Clustering 유형은 다음과 같다.
- 상호 배반적 군집: 각 관찰자가 상호 배잔적인 여러 군집 가운데 하나에만 속하는 경우
- 계보적 군집: 한 군집이 다른 군집 내부에 포함되는 형태로 군집 간 중복은 없음
- 중복 군집: 두개 이상의 군집이 한 관찰자가 동시에 속하는 것이 허용되는 경우
- 퍼지 군집: 관찰치가 각 군집에 속할 확률을 표현하는 방법

"가깝다"를 어떻게 정의할 수 있을까? 하나의 유일한 답이 존재하는 것은 아니다. 데이터 안에서 우리가 찾고자 하는 것 또는 강조하고자 하는 것에 따라 달라질 수 있다. 흔히 Clustering은 "Art"라고 하는 이유이다. - 때로는 Clustering 알고리즘 보다 유사도를 어떻게 정의하는 가가 훨씬 더 중요할 수 있다. K-Means에서 K는 클래서의 개수이다.

군집화 문제는 객체 혹은 지점사이의 일정의 거리(Distance)에 기반하며 유사도라고도 한다. 유클리드 거리 (Euclidian Distance)는 다차원의 실제값을 기반으로 계산하며, m-차원 공간의 두 지점 사이의 거리로 두 지점 사이의 "평균"과 같은 개념을 가지고 있다. Non-Euclidian Distance는 지점에 대한 개념에 근간하지 않으며 평균과 같은 개념에 바탕으로도 하지 않는다. 거리함수는 다음의 조건을 만족하여야 한다.
- d(x,y) >= 0
- d(x,y) = 0 if x=y
- d(x,y) = d(y,x)
- d(x,y) <= d(x,z) + d(z,y) <---- 삼각부등성
- 특성변수 간의 차이를 기초로 한 거리 (Distance)

- Jaccard Distance

- Dissimilarity measure (0 ~ 1)

- Cosine Similarity
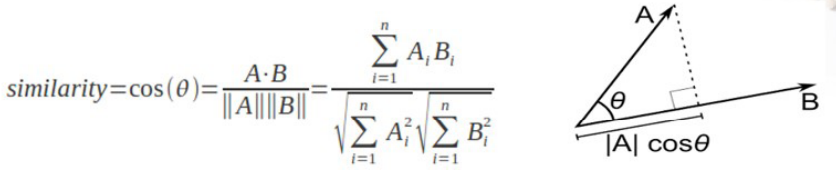
- Edit distance (편집거리 / Levenshtein distance) : 어떤 문자열을 삽입, 삭제, 변경을 하면 몇 번이나 해서 바꿀 수 있는지를 계산하여 그 최소값을 거리 판단의 척도로 사용하는 방법)
<연습문제>
아래 데이터를 사용하여 질문에 답하시오.

- 모든 조건을 다 따졌을 때
- 유클리드 거리가 가장 작은 두 사람은?
- 맨하탄거리가 가장 작은 두 사람은? - 신체조건(Age-power)만 따졌을 때 유클리드 거리가 가장 작은 조합은?
- 자동차의 보유여부가 유의한 영향을 준다고 볼 수 있는가?
클러스터링 알고리즘을 돌릴 때 데이터는 반드시 표준화해야 한다.
- Min-Max scaling : 최대값, 최소값을 0~1 scale로 조정

- Z-score/Standard scaling: 정규화 z-score로 변경
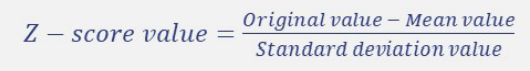
- Robust scaling: Median과 quantile을 사용하여 정규화

- Max-Absolute scaling: 절대값의 최대값과 0 이 각각 1, 0 이 되도록 조정

'데이터사이언스 > 머신러닝' 카테고리의 다른 글
| 비계층적 군집분석 (Non-hierachical Clustering) (0) | 2023.04.24 |
|---|---|
| 의사결정나무 (Decision Tree) (2) | 2023.04.22 |
| 특성공학 (Feature Engineering) 모델평가기법 (0) | 2023.04.21 |
| 머신러닝 (Machine Learning) 개요 및 유형 (0) | 2023.04.20 |
| 특성공학 (Feature Engineering) 언더피팅 / 오버피팅 (0) | 2023.04.20 |




댓글