KNN (K-Nearest Neighbors)은 K명의 가장 가까운 이웃들을 보는 알고리즘이다. 예측을 하고 싶을 때 새로운 데이터에 잘 모를 때 그 주변을 살펴보는 개념이다. 새로운 데이터에 대해 유사도를 측정하여 유사도가 높은 그룹에 들어갈 수 있도록 만들어주면 새로운 데이터를 예측할 때 이 데이터에 대해서 클러스터의 데이터에 대해 새로운 데이터를 유추해 보자는 것이다.
- 분류와 회귀문제를 모두 다룰 수 있다. 분류 문제는 다수결로 class를 예측하고, 회귀문제를 풀때는 평균값을 결과값으로 예측한다.
- 통계적 가설이 없는 비모수 방식이며 instance-based 알고리즘이다.
- Train과 Test 세트로 데이터를 분리하지만 실제로 Train은 존재하지 않는 "게으른" 알고리즘이다.
- 구체적인 데이터를 가지고 예측을 요청할때 K개의 가장 가까운 사례를 Train Data Set에서 찾아 해당하는 데이터의 y 값을 기반으로 예측 결과를 제시한다.
여기에서 실제로 여기는 지금 K 개의 가장 가까운 사례를 얘기했는데, 기본적으로 현실 세계에서 유사성이 있다는 것은 다른 한 부분도 유사성이 있다고 볼 수 있다. 일반적으로 이 사례를 많이 보는 것이 도서 구매 사이트에서 이 책을 같 본 책, 같이 구매한 책 정보를 볼 수 있었을 텐데 이것이 KNN의 개념을 활용한 것이다. 요즘 유행하는 파이썬을 살피고 있다면 한 발짝 더 들어가면 파이썬이 주로 데이터 분석 쪽에서 많이 쓰이고 있기 때문에 파이썬을 데이터 분석을 하기 때문에 데이터 분석에 관련한 파이썬 책을 추천해 주면 좋다. 그러면 이 사람을 파이썬을 좋아하면서 데이터 분석에 관심 있는 그룹으로 분류할 수 있다. 그러면 문제는 이거이다. 유사도라는 개념은 알겠는데, 데이터들끼리 유사성은 어떻게 측정할 수 있을까? 유유상종, 이웃사촌. 멀리 떨어져 있는 사촌보다 내 이웃이 더 가깝다는 것이다. 그러면 내 옆집에 사는 사람, 멀리 떨어져 있는 사존의 기준은 거리이다. 가깝다 멀다, 비슷하다 비슷하지 않다는 판단할 때 distance라는 거리를 기반으로 한다. 가깝다는 판단의 기준으로 거리를 본다. 데이터와 데이터 사이의 거리를 본다.

예를 들어 그림을 예제로 보면 노란색은 A class, 보라색은 B class. 새로운 데이타가 빨간 별이 새로 들어왔을 때 그러면 K를 3으로 놓았을 때 빨간 별과 가장 가까운 3명의 이웃을 보자. 참고로 KNN 알고리즘은 supervised 알고리즘이므로 target value를 가지고 있다. class label을 가지고 있다. 가장 가까운 3개의 데이터를 봤더니 원안에 3개가 들어왔다. 보팅을 한다. K가 3일 때 보라색이 2개, 노란색이 1개이므로 K는 B일 것이다라고 예측한다. 그런데 가만히 보니 K를 6으로 놓으면 빨간색 별이랑 6개의 이웃을 보니 노란 4개, 보라 2개 이므로 K가 6일 때는 노란색으로 예측한다. KNN 알고리즘에서는 K 값에 따라 예측 결과값이 달라진다. 그래서 투표를 할 때 동수가 나오게 되면 의사결정을 할 수 없게 된다. 그래서 K 값은 동점을 막기 위해 홀수값을 정한다. 모든 case에서 홀수는 아니고 instance가 작을 때는 K 값을 홀수로 잡는다. 데이터가 많을 경우에는 정확히 같게 나오는 경우가 거의 없기 때문에 꼭 홀수로 잡지 않아도 된다.

KNN 알고리즘을 분류 회귀 모두 사용할 수 있다. 그래서 분류문제에서는 가장 가까운 이웃을 보면서 A 인지 B 인지 예측할 수 있고 분류 문제를 풀수 있다. 그림을 보면 K가 1일 때 그림과 K가 15일 때 그림이 있다. K가 1일 때 그림을 잘 보면 지금 빨간색점과 초록색점을 모두 맞추고 있다. 즉 현재 보고 있는 데이터를 너무 잘 맞추는 오버피팅 발생한다. 그래서 실제로 K를 1로 놓았을 때는 모든 입력 데이터에 대해 모두 100%로 분류해 준다. 현업에서는 K가 1일 때는 돌리지 않는다. K 값이 작으면 작을수록 오버피팅 가능성이 높아지고, 역으로 K 값이 커지면 커질수록 모델은 단순해지기는 하지만 성능이 떨어지는 언더피팅이 발생한다. 회귀는 특정한 수치형 데이터를 예측하는 것이므로 같은 클러스터 안의 데이터들이 모두 수치형 데이터이므로 그 값들의 평균값으로 결과값을 예측한다. 분류보다는 성능이 좀 떨어진다.

유사도를 측정할때 distance를 기반으로 하는 거리를 기반으로 하는데, 일반적으로 제일 많이 쓰는 거리를 구하는 개념이 유클리드안 디스턴스 개념이다. 이차원 평편에서 두 점사이의 최단거리를 공식이다. P 자리에 P의 2가 들어오면 유클리디안 디스턴스이고 P가 1이면 맨해튼 디스턴스이다. 일반적인 거리를 구할 때는 유클리디안 디스턴스이고, 시험 문제에서는 주로 맨해튼 디스턴스가 나온다. 맨해튼 디스턴스는 기준이 되는 각각 X에서 X를 빼주고, Y에서 Y를 뺀 값에 절대값을 다 더해주면 된다. P가 1이냐 2냐에 따라 맨해튼, 유클리디안으로 달라진다.
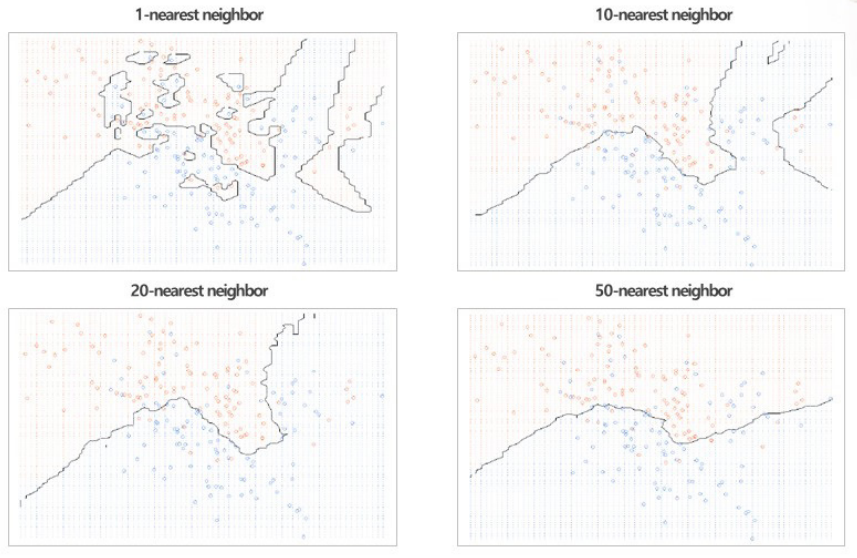
K 값이 얼마인가에 따라, 즉 1일때, 10일 때, 20일 때, 50일 때 결과는 달라진다. K 값이 증가함에 따라 굉장히 선이 단순해지고 있다. K가 1일 때는 다 맞추고 있고 오버피팅이다. 문제는 K가 언제일 때 성능이 가능 좋을지 알 수 있을까? 안타깝지만 K가 얼마일 때 가장 좋은지는 K 값을 증가시켜 가며 예측값과 target value를 비교해서 accuracy, precision, recall 등을 써서 성능을 평가하여 가장 좋은 값을 찾아야 한다. 구체적으로 K을 늘리면서 실험을 여러 번 해서 최적화된 값을 찾아야 한다.

KNN은 거리를 기반으로 하는 알고리즘이기 때문에 정규화(normalization)라는 개념을 염두해 두어야 한다. Y축에 대해서는 범위가 길기 때문에 거리를 구하는데 문제가 없지만 X축은 범위가 좁아 Y 값에 따라 거리가 결정되기 때문에 X와 Y를 함께 보는 모델에 비해 성능이 떨어질 수 있다. 정규화를 통해 X축의 범위를 넓게 변경하는 것에 대해 고민을 해야 한다.

K 값의 변화에 따른 정확도의 변화를 보면 Error가 작으면 작을 수록 좋은 것이다. 최적의 K 값을 찾는 것은 쉽지 않다. 지금처럼 K 값을 증가시켜 가면서 실험을 여러 번 돌려보는 방법밖에 없다. 그래서 그래프를 항상 그려봐야 한다. K를 50 정도까지 올려봤더니 K가 8일 때 에러가 가장 낮은 것을 알 수 있다. 그런 후 문서화를 하여 다음에 분석할 때 참고할 수 있도록 해야 한다.
KNN 알고리즘을 이해하면서 장점과 단점을 정리하면 다음과 같다.
- 장점
- 단순한 알고리즘으로 이해하기 쉽고 해석하기 쉬움
- 데이터에 대한 기본 가정이 없으므로 비선형 데이터에 매우 유용
- 분류와 회귀 모두에 사용 가능하고 이상값 찾기에도 활용 가능
- 대체로 우수한 결과를 보여줌 - 단점
- 상대적으로 높은 계산 비용
- 데이터 양이 매우 큰 경우 계산 속도가 느리고 데이터 지역 구조에 민감
- 최적의 K 값을 정하는 것이 쉽지 않다.
. K가 너무 작은 값이면 잡음에 대한 영향을 받을 가능성 (Overfitting)
. K가 너무 큰 값이면 지나치게 평활될 가능성 (Underfitting)
KNN을 계산하는 예제 문제를 풀어보면 다음 주어진 좌표값이 다음과 같을때 새로운 좌표 (2,3)은 어느 그룹에 속하겠는가? (k=3일 때로 가정)


K가 3일때 가장 가까운 좌표는 첫 번째, 두 번째, 세 번째 좌표이다. 이때 속할 클래스에 대해 투표를 실시하면 B가 다수이므로 좌표 (2,3)은 B로 예측한다.
'데이터사이언스 > 머신러닝' 카테고리의 다른 글
| 머신러닝 (Machine Learning) 개요 및 유형 (0) | 2023.04.20 |
|---|---|
| 특성공학 (Feature Engineering) 언더피팅 / 오버피팅 (0) | 2023.04.20 |
| 나이브 베이즈 (Naive Bayes) (1) | 2023.04.19 |
| 로지스틱 회귀분석 (Logistic Regression) (0) | 2023.04.16 |
| 머신러닝 선형회귀분석 (Linear Regression) (0) | 2023.04.15 |




댓글