1. 분류 (Classification) 개요
회귀분석은 target value가 수치형 변수이다. 로지스틱 회귀분석은 Y 값에 수치형 값이 나타나긴 하지만 특정한 값을 예측하는 것이 아니라 classification 문제를 풀어준다. 대부분 2 분류 문제를 풀어준다. Supervised Learning의 일종으로 입력 데이터에 존재하는 Feature 값들과 label 값의 class 간의 관계를 학습하여 새로 관측된 데이터의 class를 예측하는 문제를 풀어준다. 다음과 같은 영역에 활용할 수 있다.
- 이메일 Spam 분류
- 고객 이탈 방지
- 어느 고객이 떠날 것인가? -> 떠날 위기에 있는 고객들 대상으로 고객 유지 마케팅 수행
- 이동통신회사, FedEx, 체이스은행, 위키피디아 등등
- HR 직원 행동 예측
- 이직, 퇴사, 입사 등 직원의 행동 예측 -> 적절한 인력 관리에 활용
- HP, CIA, Linkedin, 국내 생명보험회사 등등
회귀(Regression)와 분류(Classification)는 문제를 푸는 다른 방법이다.

- 독립변수 기온, 종속변수 판매량의 경우 수치형 독립변수, 수치형 종속변수 이므로 Regression으로 푼다.
- 독립변수 위치, 요일, 종속변수 판매량의 경우 범주형 독립변수, 수치형 종속변수이므로 Regression으로 푼다.
- 독립변수 판매량, 종속변수 위치의 경우 수치형 독립변수, 범주형 종속변수이므로 Classification으로 푼다.
- 독립변수 위치, 요일, 기온, 종속변수 판매량 200 이상여부의 경우 수치형 + 범주형 독립변수, 범주형 종속변수이므로 Classification으로 푼다.
2. 로지스틱 회귀분석 (Logistic Regression)
회귀분석은 입력데이터들에 대해 추세를 잘 맞춰주는 반면, positive / negative 두 개로 분류하기 어렵다. 선을 변환시켜 변환된 곡선으로 만들면 추세를 따라가면서 분류도 가능해진다. 즉 로지스틱 회귀분석은 이진분류의 일종으로 Label 값이 0/1, Y/N 등과 같이 두 가지 class 만이 가능한 회귀분석이다. 분석 프로세스는 다음과 같다.
- 독립변수들의 선형 결합과 종속변수의 class 간의 확류적 관계를 학습
- gradient descent로 최적화된 coefficient와 intercept를 계산
- treshhod 값을 조절하여 positive class와 negative class를 어떻게 나눌지를 설정

예를 들면 GPA와 Adimission 합격여부에 대해 GPA가 높을수록 (합격) 승간이 높다는 것을 분석하고자 할 때 회귀를 통해 다음을 확인할 수 있다. 이것을 그래프로
- 합격여부와 GPA 간의 양의 상관관계는 존재한다.
- GPA 점수로 합격 여부 예측 --> GPA 점수로 합격 확률


회귀식 형태의 모델을 사용하면 각 독립변수의 통계적 유의성을 확인하고, 종속변수에 미치는 영향력 분석은 가능하다. 일반 선형회귀에서 요구하는 (-) 무한대에서 (+) 무한대인 출력값을 로지스틱 회귀분석에서는 0에서 1 사이의 출력값이 되도록 적절한 변환이 필요하다.

로지스틱 회귀분석에서는 Y 값을 확률로 본다. 특별한 얘기가 없으면 기준점이 0.5이다. 그래서 0.5 보다 작으면 A, 크면 B로 하자고 하며 이렇게 되면 분류 문제를 해결할 수 있다.
로지스틱 회귀의 변환과정은 다음과 같다. 시작은 선형회귀에서 시작한다. y 값이 확률이므로 p로 변환하고, p를 승산비(odds)로 변환한다. 그러면 y 값은 0에서 (+) 무한대 값이 된다. 이것을 로그를 취하면 로짓함수가 되며 그러면 (-) 무한대에서 (+) 무한대 값이 나온다. 이것을 역함수를 취하면 0에서 1의 값으로 정리된다.

Logit 함수에 일반 선형회귀 분석 적용한다.

비용함수(Cost Function) 은 우도(Likelihood)를 최대화하고 Cross-entropy는 최소화하는 방향으로 찾아야 한다.

비용함수로 흔히 썼었던 MSE를 안쓰는 이유는 Local minima 가 있어서 여기에 걸리게 되면 더 이상 학습이 안 되는 문제점이 있기 때문이다. Cross-entropy를 쓰면 Global minima와 Loca minima 가 한 곳에 모이기 때문 값이 적어지는 방향으로 분석이 가능하다.

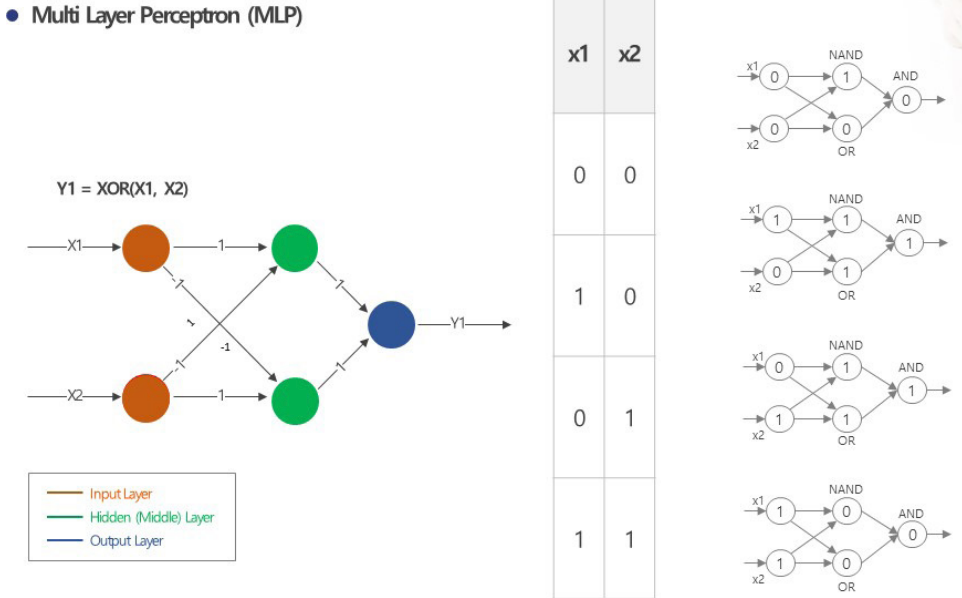
Perceptron은 신경망의 시초모델로 선형모델과 연결된다. 선을 그어 2개로 분류하는 모델이 선형분류 모델인데 XOR GATE는 선하나로 분류 불가능하다. 즉 XOR 문제를 못 푼다.

Multi Layer Perceptron (MLP)는 Multi Layer를 통해 이진분류가 가능한 선형모델이다. Perceptron은 이진 분류로 한정된다. 3차원 이상으로 확장하려면 신경망으로 넘어가야 한다.
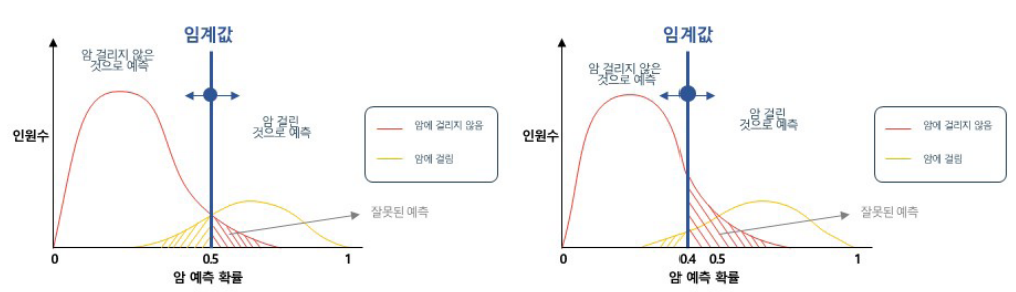
로지스틱 함수가 나왔을 때 0과 1을 분류하는 기준인 임계값(thresholds)은 기본적으로 0.5를 둔다. 임계값을 낮추면 민감도(recall)가 높아져 오분류가 높아지더라도 Y=1인 경우를 최대한 분류하게 되고, 반다래 임계값을 높이면 정확도(Precision)가 높아져 알파오류를 최소화하는 경향이 있다.
회귀분석(Regression)과 비교하면, 선형회귀에서 종속변수는 y값 자체이며, 회귀계수는 해당 독립변수 값이 1 단위 증가할때 종속변수 y의 변화량으로 증가하고, 비용함수는 예측오차의 최소화이다. 로지스틱 회귀에서 종속변수는 logit 확률로 부터 도출한 class 값이며, 회귀계수는 해당 독립변수 값이 1 단위 증가할 때 log(odds) 변화량이고, 비용함수는 cross entropy의 최소화 혹은 log likelyhood의 최대화이다.
3. 평가지표
예측대상이 범주형 데이터인 경우 분류모델의 평가 지표인 기본적으로 Precision, Recall, Accuracy, F1, G를 사용한다.
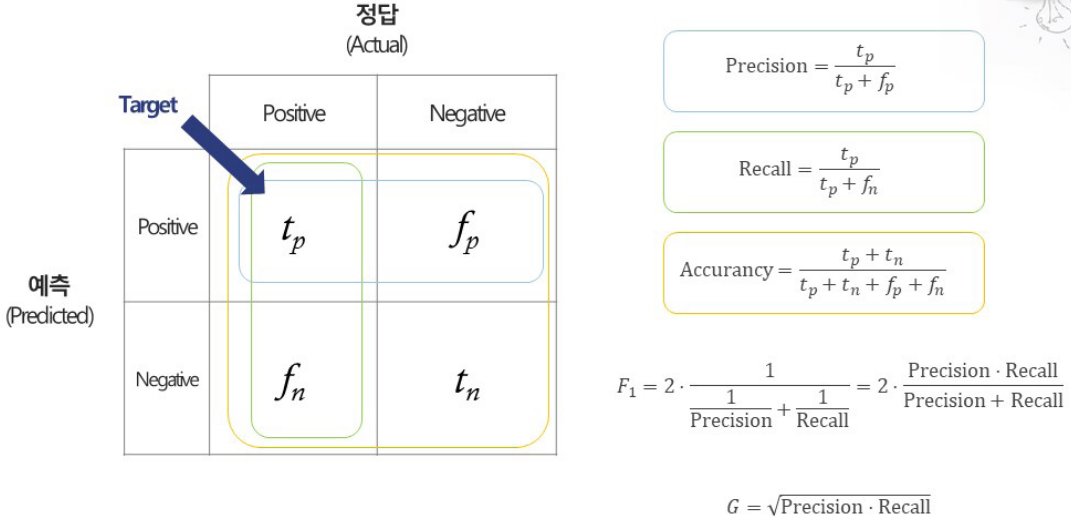
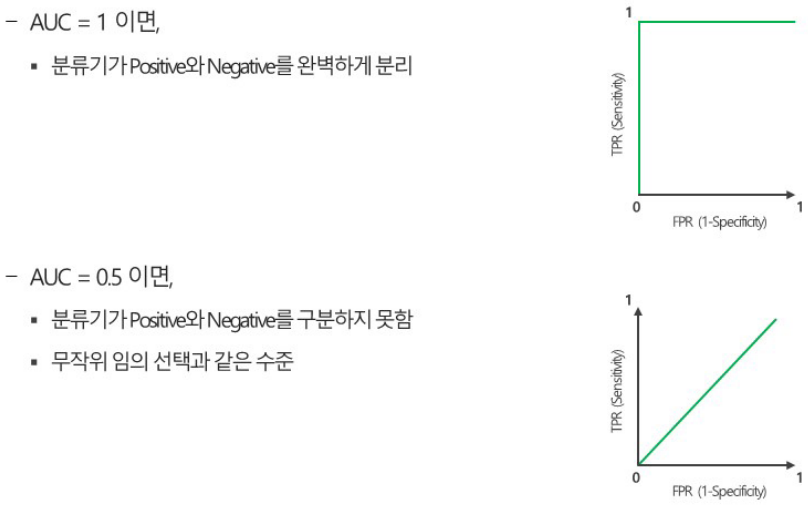
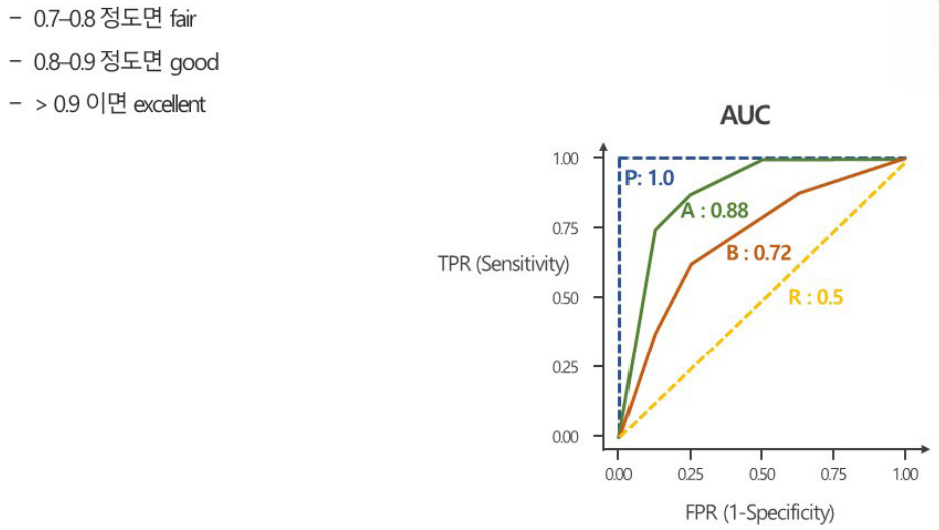
추가로 ROC (Receiver Operating Charateristic)와 AUC (Area Under the Curve)를 사용한다. TPR = TP / (TP+FN), FPR=FP / (FP + TN)으로 계산한다.

'데이터사이언스 > 머신러닝' 카테고리의 다른 글
| 머신러닝 (Machine Learning) 개요 및 유형 (0) | 2023.04.20 |
|---|---|
| 특성공학 (Feature Engineering) 언더피팅 / 오버피팅 (0) | 2023.04.20 |
| 나이브 베이즈 (Naive Bayes) (1) | 2023.04.19 |
| KNN (K-Nearest Neighbors) 알고리즘 (0) | 2023.04.16 |
| 머신러닝 선형회귀분석 (Linear Regression) (0) | 2023.04.15 |




댓글