데이터 전처리_변환 (Transformation)

데이터 변환의 개념에는 모양변환이 있다. Pivot은 행, 열별 요약된 값으로 정렬해서 분석을 하고자 할 때 사용하는 것이고, Unpivot은 칼럼 형태로 되어 있는 것을 행형태로 바꿀 때 사용 (wide form -> long form) 하는 것이다.

파생변수는 이미 수집된 변수를 활용하여 새로운 변수를 생성하는 개념을 말한다. 여기서 중요한 것은 새로운 변수를 만드는 것이다. 일반적으로 데이터를 전처리한다라고 할 때 기존에 있는 데이터를 잘 정리하는 것도 있지만 파생변수를 만드는 것에 집중한다. 분석자가 특정조건을 만족하거나 특정함수에 의해 값을 만들어 의미를 부여한 변수로 주관적일 수 있으며 논리적 타당성을 갖추어 개발해야 한다. 예를 들어 주 구매매장, 구매 다양성을 얘기할 때, 많이 가는 매장이 주 구매매장인데 몇 번 이상을 많이로 판단할 것인지 기준이 주관적일 수 있다. 이것이 논리적인 타당성을 갖기 위해서는 평균보다는 몇% 이상을 주 구매매장으로 한다는 식으로 정해야 한다.

요약변수는 빈도를 카운트한다는 개념으로 원 데이터를 분석 needs 에 맞게 종합한 변수이다. 데이터의 수준이 달리하여 종합하는 경우가 많으며, 예를 들면  총 구매금액, 매장별 방문 횟수 같은 것이 있다. 일반적으로 파생변수는 새로 만든 변수이고 요약변수는 집계의 개념이 있다고 정리할 수 있다.

데이터를 변환하는 방법인 Normalization은 데이터의 속성값이 -1.0~1.0과 같이 정해진 구간 내에 들도록 하는 기법이다.

Min-Max scaling (최대 최소 변환)은 어떤 데이터가 들어오든 간에 그 데이터의 범위를 0과 1 사이로 변환시키는 방법이고 실제로 많이 쓴다. 분모를 데이터 셋의 가장 큰 값 빼기 가장 작은 값, 분자는 입력 데이터 빼기 가장 작은 값으로 계산하면 그 값은 0과 1 사이의 범위에 떨어진다. Scale이 다른 여러 변수에 대해 scale을 맞춰 모든 데이터 포인트가 동일한 정도의 중요도로 비교되도록 하며, scaling 여부가 모델링의 성능에도 영향을 주기도 한다.

Standard Z Scaling 은 정규형을 표준정규형으로 바꾸는 개념이다. 정규는 중심이 평균이고 1 시그마, 2 시그마, 3 시그마만큼 분포되어 있는데, 문제는 정규이긴 한데 첨도가 다를 수 있다. 첨도가 달라지면 이 데이터들이 폭이 좁아진다. 정규형태이긴 한데 넓게 퍼진 경우도 있고 좁게 올라간 경우가 있을 수 있는데, 간격이 일정하지 않다. 다른 scaling을 쓰기 때문이다. 서로 다른 scale을 가지고 있는 정규분포를 같은 scale으로 변환한 것을 표준정규분포이다. 중심값이 평균에서 0으로, 표준편차는 1 시그마, 2 시그마, 3 시그마에서 1, 2, 3의 분포로 변환한 것이 표준 정규분포이다. 중심을 0으로 만들기 위해서는 평균을 빼주면 되고,  1 시그마, 2 시그마, 3 시그마를 1, 2, 3으로 바꾸기 위해서는 표준편차를 나누어 준다.

 

Normalization (정규화)는 단위 차이, 극단값 등으로 비교가 어렵거나 왜곡이 발생할 때 표준화하여 비교 가능하게 만드는 방법이다. 대표적인 Normalization 방법은 다음과 같다.

원래 데이터를 스케일링 방법으로 만들어 놓았더니 원본 데이터가 가지고 있는 특징들을 그대로 유지하면 같은 범위 안으로 만들어주는 것을 그림으로 확인할 수 있다.

Normalization 예제로 이런 것도 있다. X 값의 범위와 Y 값의 범위의 차이로 인해 분석에 어려움이 있다. 그 경우 Y는 그대로 펼쳐 놓고 X값의 폭을 넓히는 정규화 방법을 보여주고 있다. 아래 그림은 X값의 범위는 큰데 반해 Y 값의 범위가 작을 경우 Y의 스케일링을 넓혀주는 정규화의 예이다.

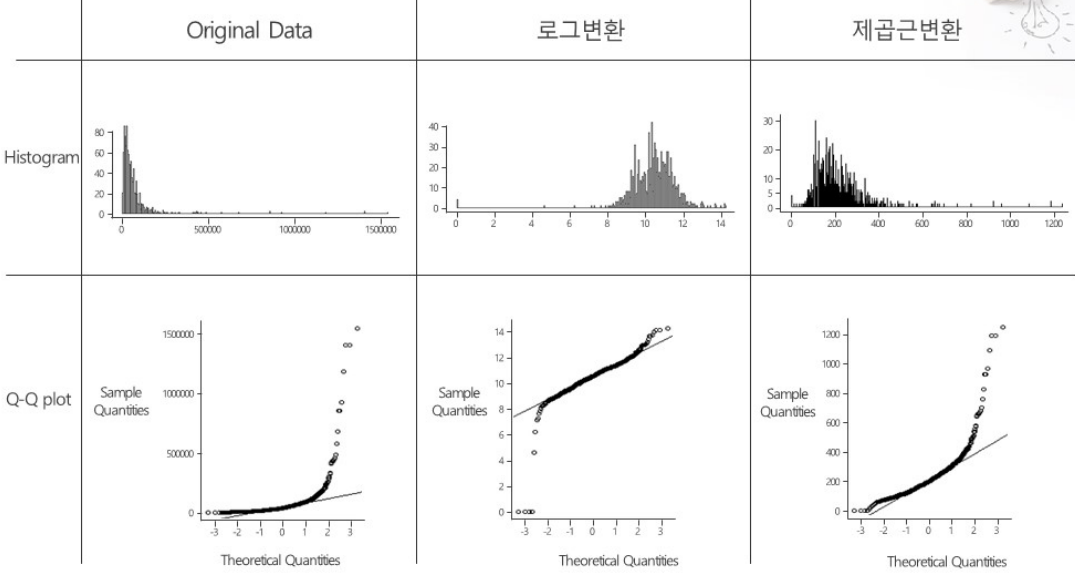
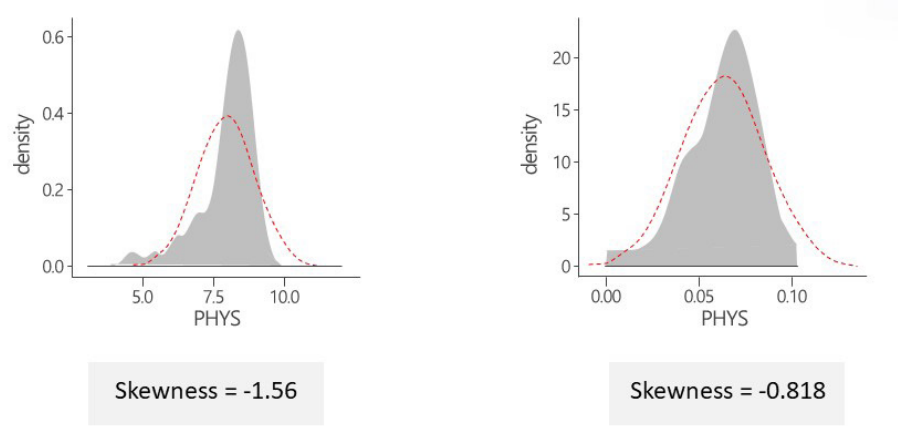
데이터 분포의 변환은 정규분포를 가정하는 분석기법을 사용할때 입력데이터가 정규를 따르지 않을 경우 정규분포 혹은 정규분포에 가깝게 변환하는 기법이다. 일반적인 통계학적 분석방법은 정규를 가정하는 경우가 생각보다 많다. 모집단은 정규분포라 하더라고 샘플 데이터는 정규를 따르지 않는 경우가 있다. 이경우 정규분포 혹은 정규분포에 가깝게 변환해야 한다.

• Positively Skewed (오른쪽 꼬리가 긴 분포): sqrt(x) -> log10(x) -> 1/x 로 변환한다.
• Negatively Skewed (왼쪽 꼬리가 긴 분포): sqrt(max(x+1)-x) -> log10(max(x+1)-x) -> 1/(max(x+1)-x) 로 변환한다.

• 종속변수의 증가가 독립변수의 증가보다 급격 : log 변환한다.
• 종속변수의 감소가 독립변수의 증가보다 급격 : square 변환한다.

 

Positvely Skewed 예 - 로그변환, 제곱근변환

 

Negatively Skewed 예 - Reflected Log10